publications

2025

1. Confined and deconfined chaos in classical spin systems

   Hyeongjin Kim, Robin Schaefer, David M. Long, and 2 more authors

   arXiv preprint arXiv:2507.07168, 2025

   Abs Bibtex HTML PDF

   Weakly perturbed integrable many-body systems are typically chaotic and thermal at late times. However, there are distinct relationships between the timescales for thermalization and chaos. The typical relationship is confined chaos: when trajectories are still confined to regions in phase space with constant conserved quantities (actions), the conjugate angle variables are already unstable. Confined chaos thus far precedes thermalization. In a different relationship, which we term deconfined chaos, chaotic instabilities and thermalization occur on the same timescale. We investigate these two qualitatively distinct scenarios through numerical and analytical studies of two perturbed integrable classical spin models: the Ishimori spin chain (confined chaos), and the central spin model with XX interactions (deconfined chaos). We analytically establish (super)-integrability in the latter model in a microcanonical shell. Deconfined chaos emerges through the separation of phase space into large quasi-integrable regions and a thin chaotic manifold. The latter causes chaos and thermalization on the fastest possible timescale, which is proportional to the inverse perturbation strength. This behavior is reminiscent of the quantum SYK models and strange metals.

   @article{kim2025confined,
     title = {Confined and deconfined chaos in classical spin systems},
     author = {Kim, Hyeongjin and Schaefer, Robin and Long, David M. and Polkovnikov, Anatoli and Chandran, Anushya},
     year = {2025},
     journal = {arXiv preprint arXiv:2507.07168},
   }

2024

1. 

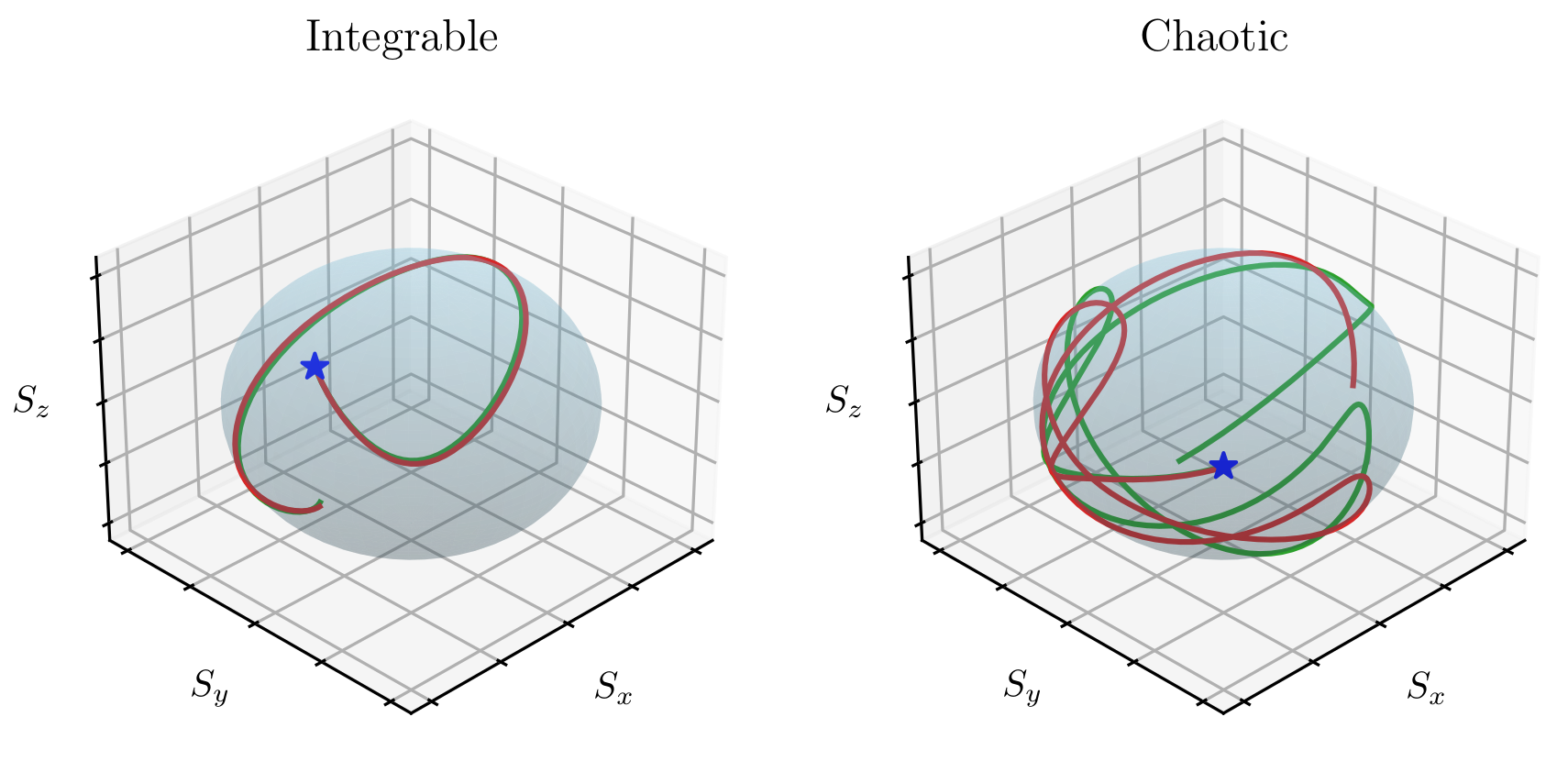   Defining classical and quantum chaos through adiabatic transformations

   Cedric Lim, Kirill Matirko, Hyeongjin Kim, and 2 more authors

   arXiv preprint arXiv:2401.01927, 2024

   Abs Bibtex HTML PDF

   We propose a formalism which defines chaos in both quantum and classical systems in an equivalent manner by means of \textitadiabatic transformations. The complexity of adiabatic transformations which preserve classical time-averaged trajectories (quantum eigenstates) in response to Hamiltonian deformations serves as a measure of chaos. This complexity is quantified by the (properly regularized) fidelity susceptibility. Physically this measure quantifies long time instabilities of physical observables due to small changes in the Hamiltonian of the system. Our exposition clearly showcases the common structures underlying quantum and classical chaos and allows us to distinguish integrable, chaotic but non-thermalizing, and ergodic/mixing regimes. We apply the fidelity susceptibility to a model of two coupled spins and demonstrate that it successfully predicts the universal onset of chaos, both for finite spin S and in the classical limit S →∞. Interestingly, we find that finite S effects are anomalously large close to integrability.

   @article{lim2024definingclassicalquantumchaos,
     title = {Defining classical and quantum chaos through adiabatic transformations},
     author = {Lim, Cedric and Matirko, Kirill and Kim, Hyeongjin and Polkovnikov, Anatoli and Flynn, Michael O.},
     year = {2024},
     journal = {arXiv preprint arXiv:2401.01927},
   }

2. 

   Variational Adiabatic Transport of Tensor Networks

   Hyeongjin Kim, Matthew Fishman, and Dries Sels

   PRX Quantum, Jun 2024

   Abs Bibtex HTML PDF

   We discuss a tensor network method for constructing the adiabatic gauge potential—the generator of adiabatic transformations—as a matrix product operator, which allows us to adiabatically transport matrix product states. Adiabatic evolution of tensor networks offers a wide range of applications, of which two are explored in this paper: improving tensor network optimization and scanning phase diagrams. By efficiently transporting eigenstates to quantum criticality and performing intermediary density-matrix renormalization group (DMRG) optimizations along the way, we demonstrate that we can compute ground and low-lying excited states faster and more reliably than a standard DMRG method at or near quantum criticality. We demonstrate a simple automated step size adjustment and detection of the critical point based on the norm of the adiabatic gauge potential. Remarkably, we are able to reliably transport states through the critical point of the models we study.

   @article{PRXQuantum.5.020361,
     title = {Variational Adiabatic Transport of Tensor Networks},
     author = {Kim, Hyeongjin and Fishman, Matthew and Sels, Dries},
     journal = {PRX Quantum},
     volume = {5},
     issue = {2},
     pages = {020361},
     numpages = {13},
     year = {2024},
     month = jun,
     publisher = {American Physical Society},
     doi = {10.1103/PRXQuantum.5.020361},
   }

3. 

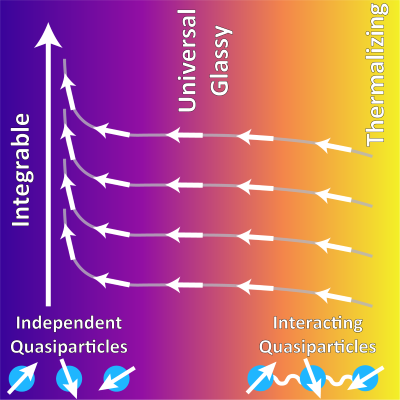   Integrability as an attractor of adiabatic flows

   Hyeongjin Kim, and Anatoli Polkovnikov

   Phys. Rev. B, May 2024

   ✍️ Editors’ Suggestion

   Abs Bibtex HTML PDF

   The interplay between quantum chaos and integrability has been extensively studied in the past decades. We approach this topic from the point of view of geometry encoded in the quantum geometric tensor, which describes the complexity of adiabatic transformations. In particular, we consider two generic models of spin chains that are parameterized by two independent couplings. In one, the integrability breaking perturbation is global while, in the other, integrability is broken only at the boundary. In both cases, the shortest paths in the coupling space lead towards integrable regions and we argue that this behavior is generic. These regions thus act as attractors of adiabatic flows similar to river basins in nature. Physically, the directions towards integrable regions are characterized by faster relaxation dynamics than those parallel to integrability, and the anisotropy between them diverges in the thermodynamic limit as the system approaches the integrable point. We also provide evidence that the transition from integrable to chaotic behavior is universal for both models, similar to continuous phase transitions, and that the model with local integrability breaking quickly becomes chaotic but avoids ergodicity.

   @article{PhysRevB.109.195162,
     title = {Integrability as an attractor of adiabatic flows},
     author = {Kim, Hyeongjin and Polkovnikov, Anatoli},
     journal = {Phys. Rev. B},
     volume = {109},
     issue = {19},
     pages = {195162},
     numpages = {16},
     year = {2024},
     month = may,
     publisher = {American Physical Society},
     doi = {10.1103/PhysRevB.109.195162},
   }